ezzy » Optionshandel » Der Optionsgrieche Delta Δ
Der Optionsgrieche Delta gilt als der wohl wichtigster „Grieche“ im Optionshandel. Beim Delta handelt es sich um die relevanteste und dennoch um eine recht einfach zu verstehende Sensitivitätskennzahl. Wenn man sich mit nur einem Griechen beschäftigen möchte, dann sollte es definitiv das Delta sein!
Delta macht die Empfindlichkeit einer Option auf Preisveränderungen im Basiswert leicht greifbar. Somit hat er in der Praxis eine große indikative Bedeutung für den Optionshandel. Die mathematisch genaue Definition lautet dabei wie folgt.
Grundsätzlich kann der Optionsgrieche Delta Werte zwischen -1 und +1 annehmen. Der Optionsgrieche Delta von Put-Optionen kann dabei zwischen -1 und 0 liegen, jener von Call-Optionen zwischen 0 und +1.
Die gängigste Interpretationsweise des Deltas ist die Ausübungswahrscheinlichkeit. Dementsprechend kann man diesen Optionsgriechen auch als die Wahrscheinlichkeit verstehen, mit der eine Option zum Laufzeitende im Geld notiert und somit ausgeübt wird.
Ein Delta von -0,2 steht bei einem Put für eine ungefähr 20%ige Wahrscheinlichkeit, dass der Put zum Ende der Laufzeit im Geld ist. Dementsprechend übt der Inhaber den Put statistisch gesehen mit 20%iger Wahrscheinlichkeit aus, sodass der Stillhalter dann seiner Kaufverpflichtung nachkommen muss. Ein Delta von +0,5 hingegen steht bei einem Call für eine ungefähr 50%ige Wahrscheinlichkeit, dass der Call zum Ende der Laufzeit im Geld ist und es zur Ausübung kommt.
Den Optionsgriechen Delta kann man dementsprechend nutzen, um einen Trade passend zur eigenen Risikofreudigkeit bzw. zum gewünschten Risikoprofil der Strategie aufzusetzen. Hier wird die Transparenz und Flexibilität im Optionshandel besonders deutlich.
Der Optionsgrieche Delta lässt sich durch mathematische Berechnungsmodelle ermitteln. In der Praxis übernimmt dies jedoch die Handelsplattform aus aktuellen Marktdaten. Da Optionspreise an freien Märkten gebildet werden und keine Bank (wie z. B. bei Optionsscheinen) zwischengeschaltet ist, können die Risikoindikatoren nicht verzerrt werden.
In der sogenannten Optionskette (siehe Abbildung unten) können die Griechen für Optionen verschiedener Basispreise und Laufzeiten eingeblendet und bequem abgelesen werden. Man bekommt durch die Delta-Spalte somit einen sehr praktischen Überblick über die Ausübungswahrscheinlichkeiten verschiedener Optionen. Zudem kann man so recht schnell erkennen, welche Optionen beispielsweise zu attraktiven Prämien gekauft bzw. verkauft werden können.
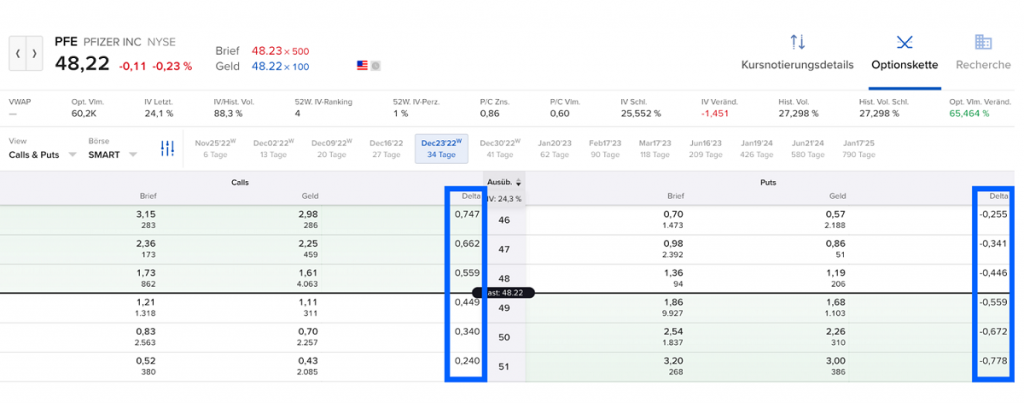
Die folgenden Abbildungen zeigen den Optionsgriechen Delta in Abhängigkeit vom Kurs des Basiswertes (hier: Pfizer; aktueller Kurs $ 48,22). Die dargestellten Diagramme beziehen sich dabei auf den 48er Put bzw. 48er Call, die beide dementsprechend nah am Geld notieren ($ 0,22 Abstand zum Strike-Preis).
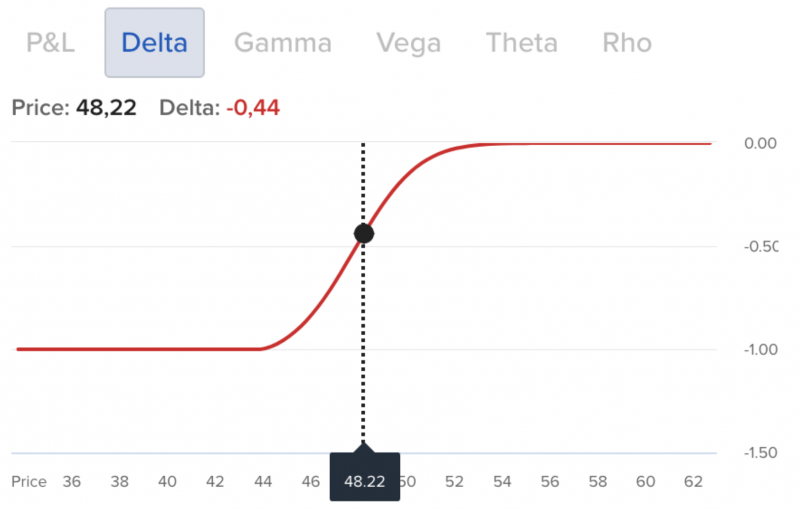
Zum aktuellen Kurs bewertet der Markt die Ausübungswahrscheinlichkeit des Puts entsprechend mit ungefähr 44 % und die des Calls mit 56 %. Würde der Aktienkurs nun bspw. auf $ 47 fallen, dann verschieben sich die Deltas dementsprechend. Der Put hätte somit ein Delta von rund -0,75. Der Optionsgrieche Delta des Calls läge hingegen bei +0,25. Demnach steigt die Ausübungswahrscheinlichkeit des Puts und die des Calls sinkt.
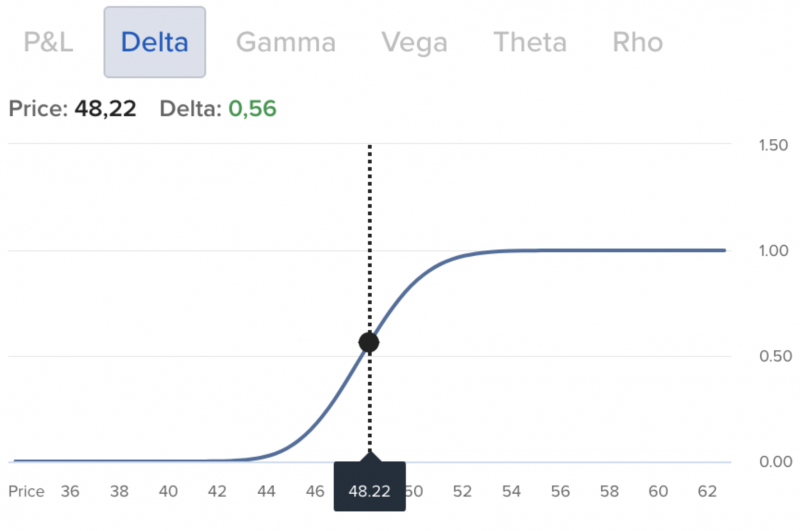
In diesem Szenario würden sich folglich auch die Preise der beiden Optionen passend dazu verändern. Dies lässt sich durch die mathematische Definition des Optionsgriechen Delta herleiten: Fällt der Kurs der Pfizer Aktie von $ 48 auf $ 47, dann entspricht dies einer Veränderung um $ -1. Bei einem Delta von -0,44 würde sich ein Put somit um $ -1 x -0,44 = $ +0,44 verteuern. Dies ist aufgrund der deutlich gestiegenen Ausübungswahrscheinlichkeit auch plausibel. Die ermittelte Preisänderung der Option muss nun noch mit dem aktuellen Optionspreis verrechnet werden. Kostet die Put-Option bspw. aktuell $ 0,76, dann wäre ihr neuer Preis $ 1,20. Der Call würde sich hingegen um $ -1 x 0,56 = $ -0,56 verbilligen. Ein um $ 1 steigender Aktienkurs auf $ 49 hätte schließlich den genau gegenteiligen Effekt.
Der Optionsgrieche Delta ist nicht nur vom Kurs des Basiswertes, sondern auch von der Restlaufzeit der Option abhängig. Die oben dargestellten Kurven verlaufen bei einer nur kurzen Restlaufzeit steiler und bei einer langen Restlaufzeit flacher. Folglich führen Preisschwankungen des Basiswertes bei kurzen Restlaufzeiten auch zu tendenziell höheren Schwankungen in der Option. Da das Delta als „Ausübungswahrscheinlichkeit“ interpretiert werden kann, ist dies auch nachvollziehbar. So kann sich die Ausübungswahrscheinlichkeit bei großen Schwankungen kurz vor Laufzeitende noch stark ändern.
Bisher gibt uns der Optionsgrieche Delta Auskunft über die Ausübungswahrscheinlichkeit einer einzelnen Option, und zwar in Abhängigkeit von Preisänderungen des Basiswertes. Damit liefert das Delta erste Anhaltspunkte, welche Risiken bspw. hinter dem Verkauf einer Put-Option mit einem bestimmten Basispreis und einer bestimmten Laufzeit stecken. Damit allein ist jedoch noch nicht klar, welches monetäre Schwankungsrisiko in der Optionsposition aktuell gebunden ist. Mit einer sehr einfachen Hochrechnung auf die gesamte Positionsgröße kann der Optionsgrieche Delta jedoch auch das leisten. Man spricht dabei im Englischen auch vom sogenannten „Position Delta“.
Position Delta = Anzahl gehaltener Optionen x Kontraktgröße (i.d.R. 100) x Delta
Das Position Delta gibt damit einen guten Anhaltspunkt für das monetäre Schwankungsrisiko einer Optionsposition, und zwar bezogen auf eine Preisveränderung im Basiswert um eine Geldeinheit (z. B. $ 1). Damit kann z. B. abgeschätzt werden, wie eine Hedging-Position gestaltet werden müsste, um die Optionsposition vor Verlusten zu schützen. Man bezeichnet den Aufbau von Hedging-Positionen, die dem Optionsgriechen Delta einer bestehenden Optionsposition entgegenwirken, als Delta-Hedging. Gelingt es, Wertschwankungen der Bestandsposition ganz zu neutralisieren, spricht man schließlich von einem Delta-neutralen Hedge.
Das könnte dich auch interessieren:
Teile diesen Beitrag bitte, wenn er dir gefallen hat:
Der Handel mit Wertpapieren und Produkten mit Hebelwirkung birgt ein hohes Risiko und kann nicht für jeden Anleger angemessen sein. Vergewissern Sie sich, dass Sie alle damit verbundenen Risiken vollständig verstanden haben. Der Handel mit Hebel Produkten kann zum Totalverlust Ihres eingesetzten Kapitals führen, und darüber hinaus Verluste nach sich ziehen. Die vollständige Risikowarnung finden Sie in unseren Risikohinweisen.
Der Optionen-Handel birgt ein erhebliches Verlustpotenzial. Das Abwicklungsdatum kann bei Optionen-Transaktionen aufgrund von Unterschieden zwischen Zeitzonen und unterschiedlichen Feiertagen variieren. Wenn Sie über verschiedene Optionen-Märkte hinweg handeln, kann es daher vorkommen, dass Sie sich Kapital leihen müssen, um Optionen-Transaktionen abzuwickeln.
DISCLAIMER: Die von der ezzy AG (im Folgenden ezzy) hier dargestellten Informationen dienen nur zu Informationszwecken und stellen keine Aufforderung zum Kauf oder Verkauf von Wertpapieren oder Finanzinstrumenten dar. ezzy kann trotz sorgfältiger Arbeitsweise keine Haftung für irrtümliche oder fehlerhafte Inhalte übernehmen. Ein öffentliches Angebot zum Erwerb von Wertpapieren oder Finanzinstrumenten wird von ezzy generell nicht unterbreitet. Mit der Erstellung von Texten und der Weitergabe von Informationen ist ezzy nicht als Vermögens- oder Anlageberater tätig. Alle Entscheidungen bezüglich des Erwerbs oder Verkaufs von Wertpapieren und Finanzinstrumenten sollte auf Grundlage eines individuellen Beratungsgespräches mit dem Bankberater und eines entsprechenden Prospektes getroffen werden.
Durch die weitere Nutzung der Seite stimmst du der Verwendung von Cookies zu. Weitere Informationen
Die Cookie-Einstellungen auf dieser Website sind auf "Cookies zulassen" eingestellt, um das beste Surferlebnis zu ermöglichen. Wenn du diese Website ohne Änderung der Cookie-Einstellungen verwendest oder auf "Akzeptieren" klickst, erklärst du sich damit einverstanden.
