ezzy » Optionshandel » Der Optionsgrieche Vega
Genau wie die anderen Griechen Delta, Gamma und Theta beschreibt auch der Optionsgrieche Vega einen Einflussfaktor auf den Preis einer Option: den Faktor Volatilität (Merkhilfe: Vega wie Volatilität).
Der Optionsgrieche Vega beschreibt also, wie stark sich der Optionspreis verändert, wenn sich die Implizite Volatilität des Basiswerts um einen Prozentpunkt ändert (auch hier gilt die Prämisse ceteris paribus, das heißt unter der Annahme, dass alle anderen Faktoren gleich bleiben).
Vereinfacht kann man festhalten, dass eine steigende Implizite Volatilität auch zu höheren Optionspreisen führt: Höhere Schwankungen erhöhen schlicht das Risiko der Optionsausübung. Das wiederum schlägt sich in einem höheren Optionspreis nieder. Oder anders ausgedrückt: Die Absicherung gegen fallende bzw. steigende Kurse wird für den Optionskäufer teurer – und für den Optionsverkäufer (Stillhalter) besser bezahlt. Umgekehrt führt eine sinkende Implizite Volatilität zu tendenziell sinkenden Optionspreisen.
Für die Verkäuferseite einer Option, das heißt für Short Put– und Short Call-Positionen, ist eine sinkende Volatilität günstig. Denn bei sinkender Volatilität kann die initial verkaufte Optionsposition durch den sinkenden Optionspreis oft günstiger zurückgekauft werden. Für die Käuferseite wiederum, das heißt für Long Puts und Long Calls, ist hingegen eine steigende Volatilität günstig. Denn die dadurch tendenziell steigenden Optionspreise erhöhen den Wert der Long-Positionen.
Die Pfizer-Aktie notiert aktuell bei $48,22. Wir betrachten eine Option mit einer Impliziten Volatilität von aktuell 50%. Die Option kostet aktuell $1,20 und der Markt bewertet das Vega dieser Option mit 0,09.
Erklärung: Für den Inhaber der Option (Long-Position) ist das positiv, denn für ihn steigt die Option im Wert. Besitzt er sie allerdings noch nicht, so muss er beim Kauf einen höheren Preis bezahlen. Für den Stillhalter (Short-Position) wiederum zeigt sich ein gegenteiliges Bild, denn seine Position verliert an Wert. Das heißt, er ist „short“ in der Option, daher wirkt sich ein Wertanstieg negativ für ihn aus. Hat er die Option noch nicht verkauft, wird er beim Verkauf einen höheren Preis erzielen.
Erklärung: Für den Inhaber der Option (Long-Position) ist das negativ, denn für ihn sinkt die Option im Wert. Besitzt er sie allerdings noch nicht, dann kann er sie für einen günstigeren Preis kaufen. Für den Stillhalter (Short-Position) wiederum zeigt sich auch hier ein gegenteiliges Bild, denn seine Position gewinnt an Wert. Er ist „short“ in der Option, daher wirkt sich ein Wertverfall positiv für ihn aus. Hat er die Option noch nicht verkauft, kann er beim Verkauf allerdings nur eine geringere Prämie einnehmen.
Der Optionsgrieche Vega ist grundsätzlich um den Strike-Preis am größten. Hier ist der Optionspreis am sensitivsten, wenn sich die erwartete Volatilität ändert. Bei Optionen, die tiefer im Geld oder tiefer aus dem Geld notieren, nimmt der Einfluss der Volatilität und somit auch das Vega ab.
Wie bei den anderen Griechen hat auch die Restlaufzeit einen Einfluss auf den Optionsgriechen Vega. Denn je kürzer die Restlaufzeit, desto geringer ist der Einfluss der Volatilität auf den Optionspreis. Bei der Herleitung hilft auch hier die Versicherungsanalogie: Möchte man ein Risiko versichern (das „Risiko“ wird hier durch die Implizite Volatilität repräsentiert), ist der Preis für die Versicherung (Optionspreis) bei einer längeren Laufzeit höher. Dies trifft umso mehr zu, je höher die erwartete Schwankung ist – und schlägt sich in einem hohen Vega nieder.
Die folgenden drei Abbildungen zeigen je eine Put-Option auf Pfizer mit Strike-Preis $48. Durch den aktuellen Aktienkurs von $48,22 sind alle Optionen nahe am Geld. Unterschiedlich sind allerdings die jeweiligen Restlaufzeiten von 5, 30 und 90 Tagen.
Die Option mit der längsten Restlaufzeit (90 Tage, Abb. 1) weist den flachsten Verlauf im Optionsgriechen Vega auf. Das Vega ist direkt um den Strike-Preis am größten. Das heißt, die am längsten laufende Option hat das größte Vega. Hier hat eine Veränderung der Impliziten Volatilität während der Laufzeit also den größten Effekt. Nimmt die Implizite Volatilität bei dieser Option um einen Prozentpunkt ab, so verliert die Option -$0,09 an Wert.
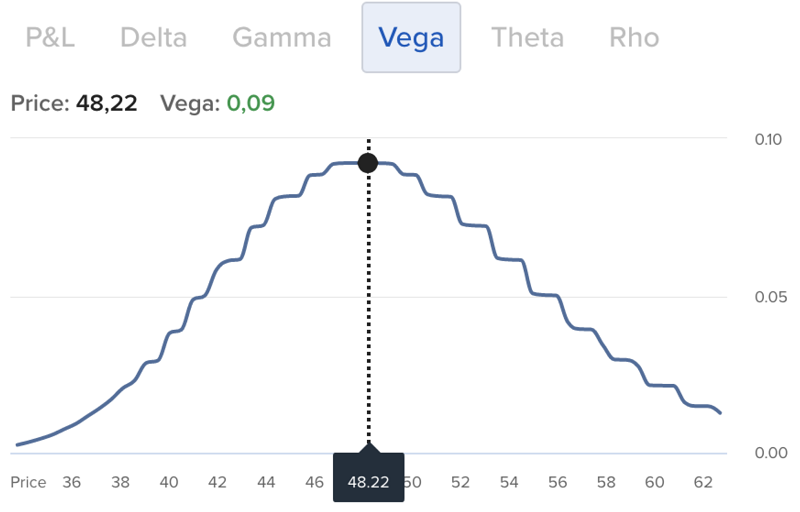
Bei der Option mit kurzer Restlaufzeit von nur 5 Tagen hat der Optionsgrieche Vega einen wesentlich geringeren Einfluss, der wiederum in der Region des Strike-Preises am größten ist.
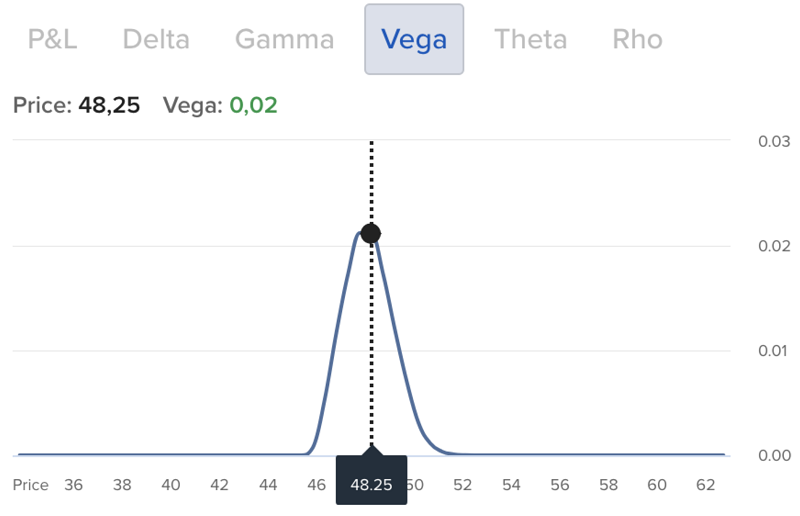
Die Optionskette bietet wie bei allen Griechen auch für den Optionsgriechen Vega eine angenehme Übersicht.
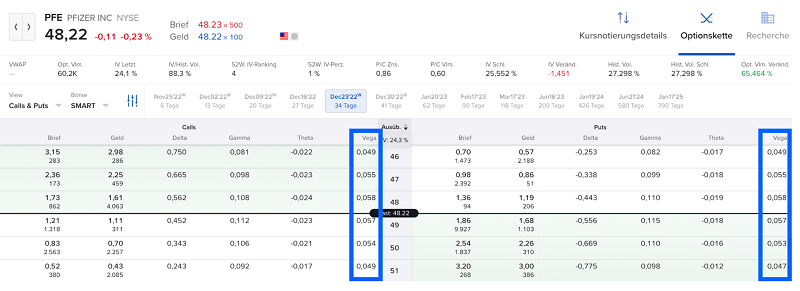
Teile diesen Beitrag bitte, wenn er dir gefallen hat:
Der Handel mit Wertpapieren und Produkten mit Hebelwirkung birgt ein hohes Risiko und kann nicht für jeden Anleger angemessen sein. Vergewissern Sie sich, dass Sie alle damit verbundenen Risiken vollständig verstanden haben. Der Handel mit Hebel Produkten kann zum Totalverlust Ihres eingesetzten Kapitals führen, und darüber hinaus Verluste nach sich ziehen. Die vollständige Risikowarnung finden Sie in unseren Risikohinweisen.
Der Optionen-Handel birgt ein erhebliches Verlustpotenzial. Das Abwicklungsdatum kann bei Optionen-Transaktionen aufgrund von Unterschieden zwischen Zeitzonen und unterschiedlichen Feiertagen variieren. Wenn Sie über verschiedene Optionen-Märkte hinweg handeln, kann es daher vorkommen, dass Sie sich Kapital leihen müssen, um Optionen-Transaktionen abzuwickeln.
DISCLAIMER: Die von der ezzy AG (im Folgenden ezzy) hier dargestellten Informationen dienen nur zu Informationszwecken und stellen keine Aufforderung zum Kauf oder Verkauf von Wertpapieren oder Finanzinstrumenten dar. ezzy kann trotz sorgfältiger Arbeitsweise keine Haftung für irrtümliche oder fehlerhafte Inhalte übernehmen. Ein öffentliches Angebot zum Erwerb von Wertpapieren oder Finanzinstrumenten wird von ezzy generell nicht unterbreitet. Mit der Erstellung von Texten und der Weitergabe von Informationen ist ezzy nicht als Vermögens- oder Anlageberater tätig. Alle Entscheidungen bezüglich des Erwerbs oder Verkaufs von Wertpapieren und Finanzinstrumenten sollte auf Grundlage eines individuellen Beratungsgespräches mit dem Bankberater und eines entsprechenden Prospektes getroffen werden.

Der Kapitalkongress steht vor der Tür! Vom 13.03. bis 20.03.2025 gibt es wertvolle Insights rund um Investments und Börse.
Wir sind auch dabei und zeigen wie man mithilfe unseres Screeners schnell und effektiv gute Options-Trades findet.
Willst du dabei sein? Dann melde dich hier kostenlos an: